Галилей, Галилео 3

• Страница 0 - название энциклопедической статьи.
• Страницы 1, ... - доп. материал, указывать в "Ссылки".
• Страница: инфо , 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18 , 19 , 20 , 21 , 22 , 23 , 24 , 25

---

Античные и средневековые философы предлагали для объяснения явлений природы разнообразные «метафизические сущности» (субстанции), которым приписывались надуманные свойства. Галилея такой подход не устраивал:

Поиск сущности я считаю занятием суетным и невозможным, а затраченные усилия — в равной мере тщетными как в случае с удалёнными небесными субстанциями, так и с ближайшими и элементарными; и мне кажется, что одинаково неведомы как субстанция Луны, так и Земли, как пятен на Солнце, так и обыкновенных облаков… [Но] если тщетно искать субстанцию солнечных пятен, это ещё не значит, что нами не могут быть исследованы некоторые их характеристики, например место, движение, форма, величина, непрозрачность, способность к изменениям, их образование и исчезновение.

Декарт отверг такую позицию (в его физике основное внимание уделялось именно нахождению «главных причин»), однако начиная с Ньютона галилеевский подход становится преобладающим.

Галилей считается одним из основателей механицизма. Этот научный подход рассматривает Вселенную как гигантский механизм, а сложные природные процессы — как комбинации простейших причин, главная из которых — механическое движение. Анализ механического движения лежит в основе работ Галилея. Он писал в «Пробирных дел мастере»:

Никогда я не стану от внешних тел требовать чего-либо иного, чем величина, фигура, количество, и более или менее быстрые движения для того, чтобы объяснить возникновение ощущений вкуса, запаха и звука; я думаю, что если бы мы устранили уши, языки, носы, то остались бы только фигуры, числа, движения, но не запахи, вкусы и звуки, которые, по моему мнению, вне живого существа являются не чем иным, как только пустыми именами.

Для проектирования эксперимента и для осмысления его результатов нужна некоторая предварительная теоретическая модель исследуемого явления, и основой её Галилей считал математику, выводы которой он рассматривал как самое достоверное знание: книга природы «написана на языке математики»; «Тот, кто хочет решать вопросы естественных наук без помощи математики, ставит неразрешимую задачу. Следует измерять то, что измеримо, и делать измеримым то, что таковым не является.»

Опыт Галилей рассматривал не как простое наблюдение, а как осмысленный и продуманный вопрос, заданный природе. Он допускал и мысленные эксперименты, если их результаты не вызывают сомнений. При этом он ясно представлял, что сам по себе опыт не даёт достоверного знания, и полученный от природы ответ должен подвергнуться анализу, результат которого может привести к переделке исходной модели или даже к замене её на другую. Таким образом, эффективный путь познания, по мнению Галилея, состоит в сочетании синтетического (в его терминологии, композитивный метод) и аналитического (резолютивный метод), чувственного и абстрактного. Эта позиция, поддержанная Декартом, с этого момента утвердилась в науке. Тем самым наука получила свой метод, собственный критерий истины и светский характер.

Механика

Последний труд Галилея по основам механики

Физика и механика в те годы изучались по сочинениям Аристотеля, которые содержали метафизические рассуждения о «первопричинах» природных процессов. В частности, Аристотель утверждал:

• Скорость падения пропорциональна весу тела.
• Движение происходит, пока действует «побудительная причина» (сила), и в отсутствие силы прекращается.

Находясь в Падуанском университете, Галилей изучал инерцию и свободное падение тел. В частности, он заметил, что ускорение свободного падения не зависит от веса тела, таким образом опровергнув первое утверждение Аристотеля.

В своей последней книге Галилей сформулировал правильные законы падения: скорость нарастает пропорционально времени, а путь — пропорционально квадрату времени. В соответствии со своим научным методом он тут же привёл опытные данные, подтверждающие открытые им законы. Более того, Галилей рассмотрел (в 4-й день «Бесед») и обобщённую задачу: исследовать поведение падающего тела с ненулевой горизонтальной начальной скоростью. Он совершенно правильно предположил, что полёт такого тела будет представлять собой суперпозицию (наложение) двух «простых движений»: равномерного горизонтального движения по инерции и равноускоренного вертикального падения. Галилей доказал, что указанное, а также любое брошенное под углом к горизонту тело летит по параболе. В истории науки это первая решённая задача динамики. В заключение исследования Галилей доказал, что максимальная дальность полёта брошенного тела достигается для угла броска 45° (ранее это предположение высказал Тарталья, который, однако, не смог его строго обосновать). На основе своей модели Галилей (ещё в Венеции) составил первые артиллерийские таблицы.

Галилей опроверг и второй из приведённых законов Аристотеля, сформулировав первый закон механики (закон инерции): при отсутствии внешних сил тело либо покоится, либо равномерно движется. То, что мы называем инерцией, Галилей поэтически назвал «неистребимо запечатлённое движение». Правда, он допускал свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений). Правильную формулировку закона позднее дали Декарт и Ньютон; тем не менее общепризнанно, что само понятие «движение по инерции» впервые введено Галилеем, и первый закон механики по справедливости носит его имя.

Галилей является одним из основоположников принципа относительности в классической механике, который также был позже назван в его честь. В «Диалоге о двух системах мира» Галилей сформулировал принцип относительности следующим образом:

Для предметов, захваченных равномерным движением, это последнее как бы не существует и проявляет своё действие только на вещах, не принимающих в нём участия.

Эти открытия Галилея, кроме всего прочего, позволили ему опровергнуть многие доводы противников гелиоцентрической системы мира, утверждавших, что вращение Земли заметно сказалось бы на явлениях, происходящих на её поверхности. Например, по мнению геоцентристов, поверхность вращающейся Земли за время падения любого тела уходила бы из-под этого тела, смещаясь на десятки или даже сотни метров. Галилей уверенно предсказал: «Будут безрезультатны любые опыты, которые должны были бы указывать более против, чем за вращение Земли».

Галилей опубликовал исследование колебаний маятника и заявил, что период колебаний не зависит от их амплитуды (это приблизительно верно для малых амплитуд). Он также обнаружил, что периоды колебаний маятника соотносятся как квадратные корни из его длины. Результаты Галилея привлекли внимание Гюйгенса, который изобрёл часы с маятниковым регулятором (1657); с этого момента появилась возможность точных измерений в экспериментальной физике.

Многие рассуждения Галилея представляют собой наброски открытых много позднее физических законов. Например, в «Диалоге» он сообщает, что вертикальная скорость шара, катящегося по поверхности сложного рельефа, зависит только от его текущей высоты, и иллюстрирует этот факт несколькими мысленными экспериментами; сейчас мы бы сформулировали этот вывод как закон сохранения энергии в поле тяжести. Аналогично он объясняет (теоретически незатухающие) качания маятника.

В статике Галилей ввёл фундаментальное понятие момента силы (итал. momento).

Астрономия

Зарисовки Луны из рабочей тетради Галилея

В 1609 году Галилей самостоятельно построил свой первый телескоп с выпуклым объективом и вогнутым окуляром. Труба давала приблизительно трёхкратное увеличение. Вскоре ему удалось построить телескоп, дающий увеличение в 32 раза. Отметим, что термин телескоп ввёл в науку именно Галилей (сам термин предложил ему Федерико Чези, основатель «Академии деи Линчеи»). Ряд телескопических открытий Галилея способствовали утверждению гелиоцентрической системы мира, которую Галилей активно пропагандировал, и опровержению взглядов геоцентристов Аристотеля и Птолемея.

Первые телескопические наблюдения небесных тел Галилей провёл 7 января 1610 года. Эти наблюдения показали, что Луна, подобно Земле, имеет сложный рельеф — покрыта горами и кратерами. Известный с древних времен пепельный свет Луны Галилей объяснил как результат попадания на наш естественный спутник солнечного света, отражённого Землёй. Всё это опровергало учение Аристотеля о противоположности «земного» и «небесного»: Земля стала телом принципиально той же природы, что и небесные светила, а это, в свою очередь, служило косвенным доводом в пользу системы Коперника: если другие планеты движутся, то естественно предположить, что движется и Земля. Галилей обнаружил также либрацию Луны и довольно точно оценил высоту лунных гор.

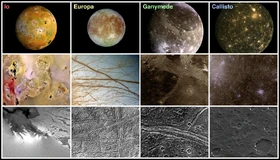
Галилеевы спутники Юпитера (современные фотографии)

У Юпитера обнаружились собственные луны — четыре спутника. Тем самым Галилей опроверг один из доводов противников гелиоцентризма: Земля не может вращаться вокруг Солнца, поскольку вокруг неё самой вращается Луна. Ведь Юпитер заведомо должен был вращаться либо вокруг Земли (как в геоцентрической системе), либо вокруг Солнца (как в гелиоцентрической). Полтора года наблюдений позволили Галилею оценить период обращения этих спутников (1612), хотя приемлемая точность оценки была достигнута только в эпоху Ньютона. Галилей предложил использовать наблюдения затмений спутников Юпитера для решения важнейшей проблемы определения долготы на море. Сам он не смог разработать реализацию подобного подхода, хотя работал над ней до конца жизни; первым успеха добился Кассини (1681), однако из-за трудностей наблюдений на море метод Галилея применялся в основном сухопутными экспедициями, а после изобретения морского хронометра (середина XVIII века) проблема была закрыта.

Галилей открыл также (независимо от Иоганна Фабрициуса и Хэрриота) солнечные пятна. Существование пятен и их постоянная изменчивость опровергали тезис Аристотеля о совершенстве небес (в отличие от «подлунного мира»). По результатам их наблюдений Галилей сделал вывод, что Солнце вращается вокруг своей оси, оценил период этого вращения и положение оси Солнца.

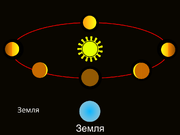
Фазы Венеры

Галилей установил, что Венера меняет фазы. С одной стороны, это доказывало, что она светит отражённым светом Солнца (насчёт чего в астрономии предшествующего периода не было ясности). С другой стороны, порядок смены фаз соответствовал гелиоцентрической системе: в теории Птолемея Венера как «нижняя» планета была всегда ближе к Земле, чем Солнце, и «полновенерие» было невозможно.

Галилей отметил также странные «придатки» у Сатурна, но открытию кольца помешали слабость телескопа и поворот кольца, скрывший его от земного наблюдателя. Полвека спустя кольцо Сатурна открыл и описал Гюйгенс, в распоряжении которого был 92-кратный телескоп.

Галилей показал, что при наблюдении в телескоп планеты видны как диски, видимые размеры которых в различных конфигурациях меняются в таком соотношении, какое следует из теории Коперника. Однако диаметр звёзд при наблюдениях с телескопом не увеличивается. Это опровергало оценки видимого и реального размера звезд, которые использовались некоторыми астрономами как аргумент против гелиоцентрической системы.

Млечный путь, который невооружённым глазом выглядит как сплошное сияние, распался на отдельные звёзды (что подтвердило догадку Демокрита), и стало видно громадное количество неизвестных ранее звёзд.

В «Диалоге о двух системах мира» Галилей подробно обосновал (устами персонажа Сальвиати), почему он предпочитает систему Коперника, а не Птолемея:

• Венера и Меркурий никогда не оказываются в противостоянии, то есть в стороне неба, противоположной Солнцу. Это означает, что они вращаются вокруг Солнца, и их орбита проходит между Солнцем и Землёй.
• У Марса противостояния бывают. Кроме того, Галилей не выявил у Марса фаз, заметно отличных от полной освещённости видимого диска. Отсюда и из анализа изменений яркости при движении Марса Галилей сделал вывод, что эта планета тоже вращается вокруг Солнца, но в данном случае Земля находится внутри её орбиты. Аналогичные выводы он сделал для Юпитера и Сатурна.

Ссылки

инфо 0 Биография 0 Ранние годы 0 Падуя, 1592—1610 0 Флоренция, 1610—1632 0 Защита коперниканства 1 Создание новой механики 1 Конфликт с католической церковью 2 Последние годы 2 Научные достижения 2 Философия и научный метод 3 Механика 3 Астрономия 4 Математика 4 Другие достижения 4 Ученики

4 Память 4 Оценки личности 4 Галилей в литературе и искусстве 4 Галилей на бонах и почтовых марках 4 Мифы и альтернативные версии 4 «И всё-таки она вертится» 4 Галилей и Пизанская башня 4 Принцип относительности и движение Солнца вокруг Земли 5 Галилей и обвинение в атомизме 5 Научные труды 5 На языке оригинала